Research
Interestes
- Optimization
- Continuous model for discrete methods
- Fast numerical solver for high order, nonlinear PDE
- Phase Field Models and Numerical Methods
- Inference on PDE and Stochastic Models
- Inverse problem
- Methods for Bayesian inference (MCMC, HMC, coupling, etc)
- Information Geometry
- Mathematical Aspect of Machine Learning and Neural Network
Publications
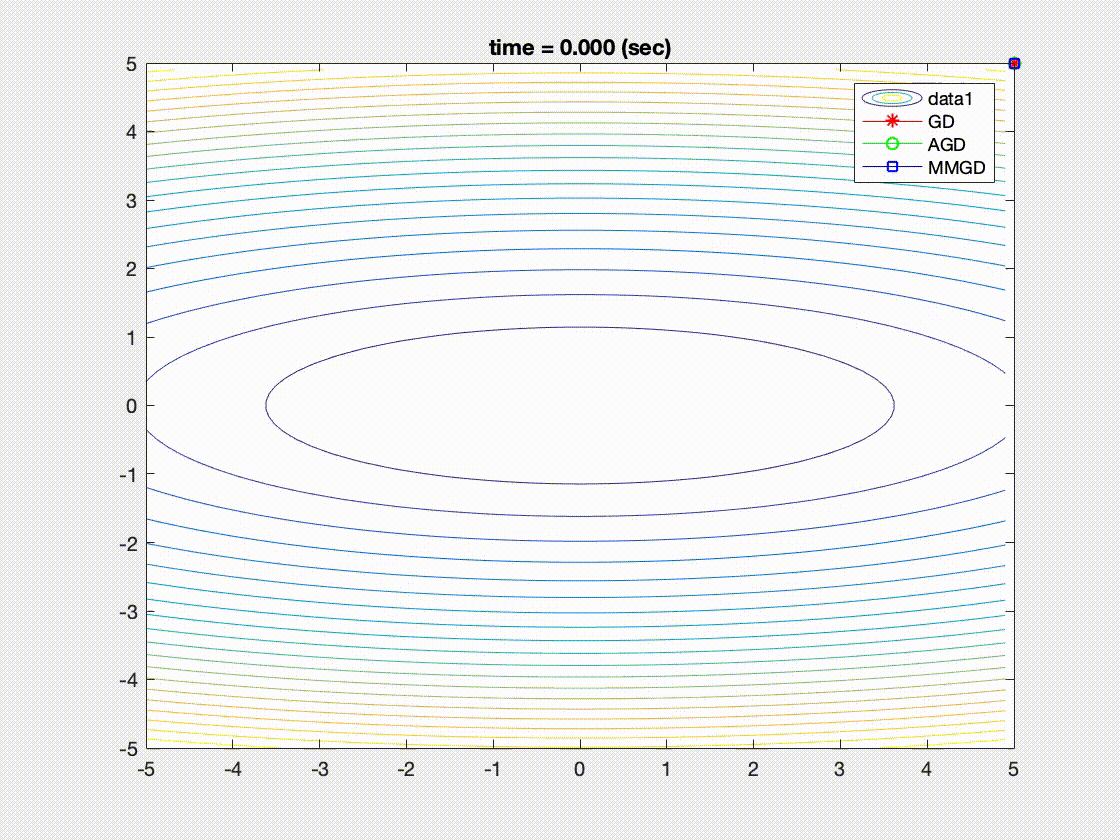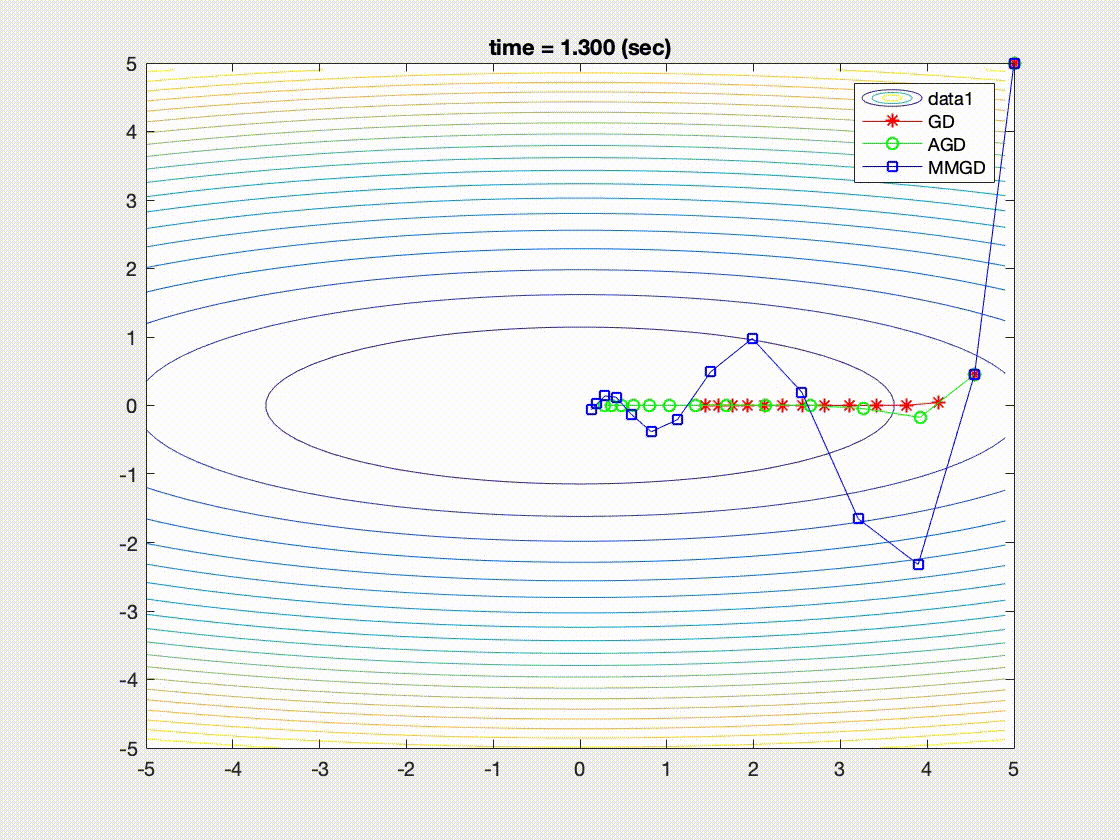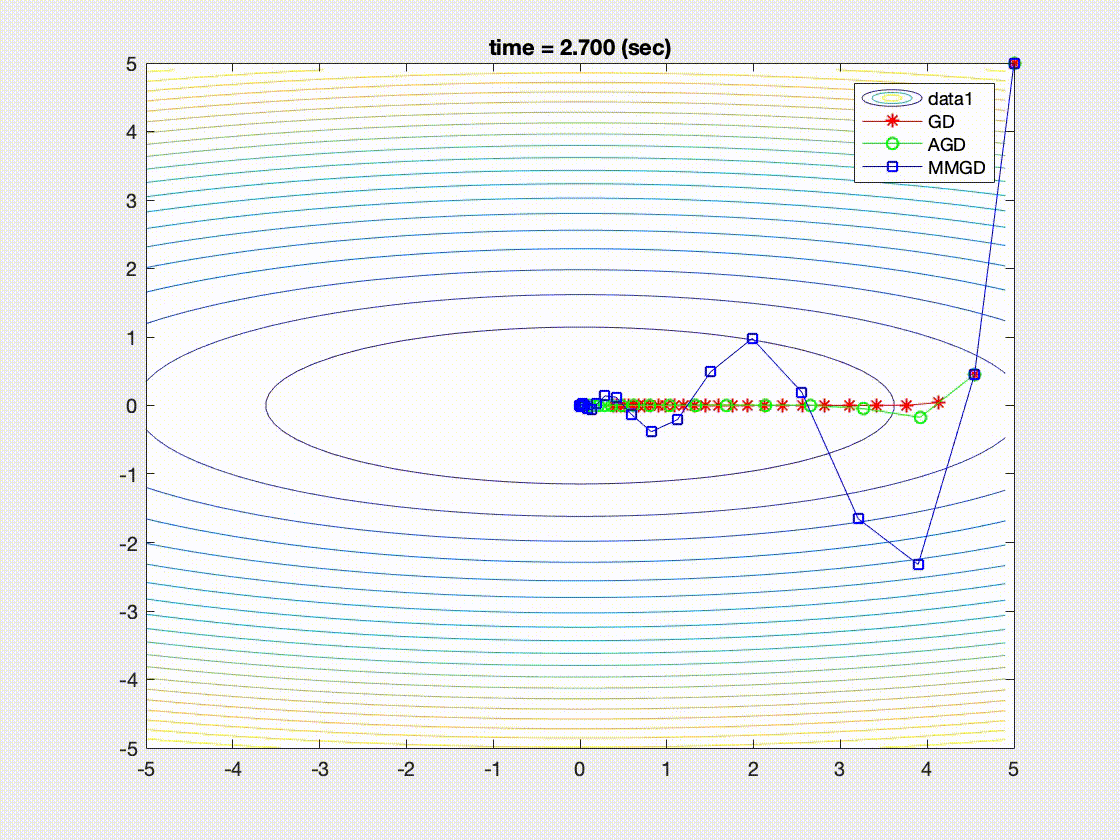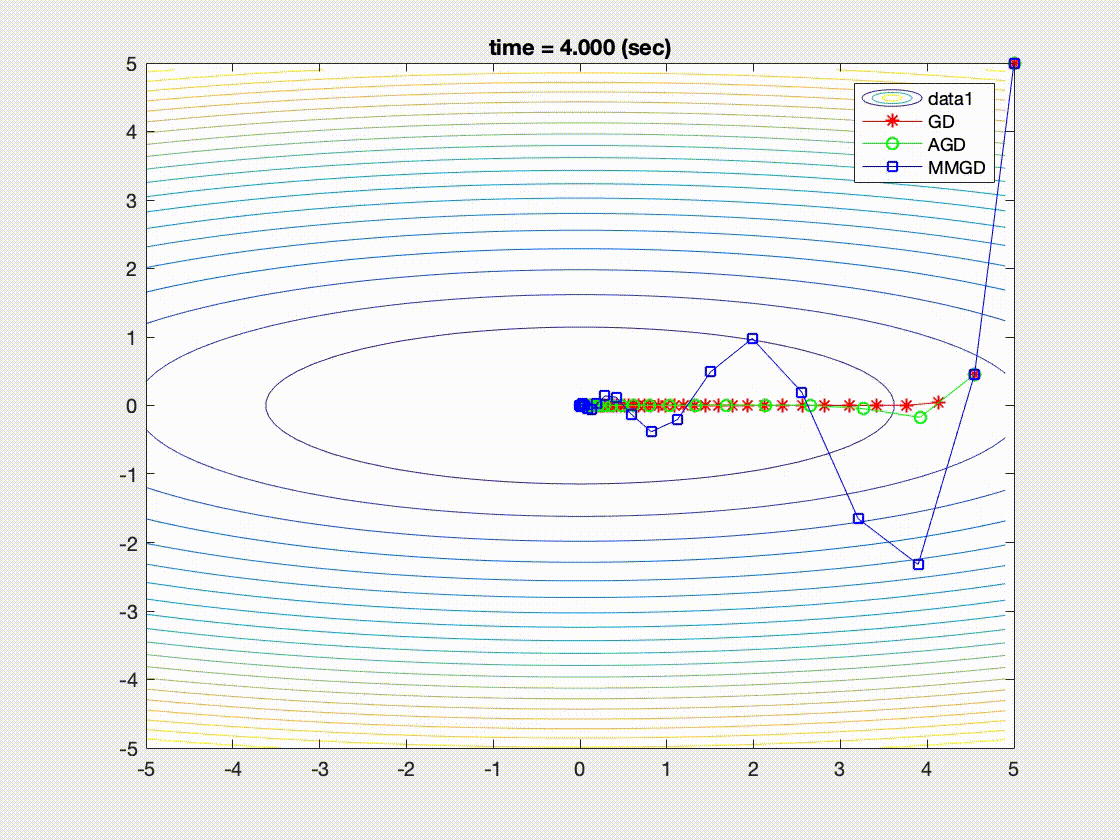 |
| Convergence behaviors of Nesterove acceleration (AGD), momentum method (MM), gradient descent (GD) [1] |
 |
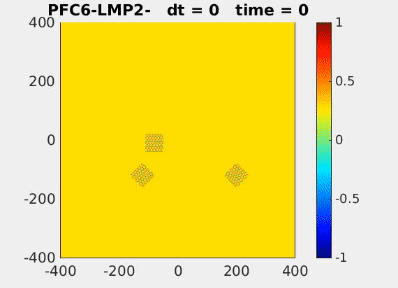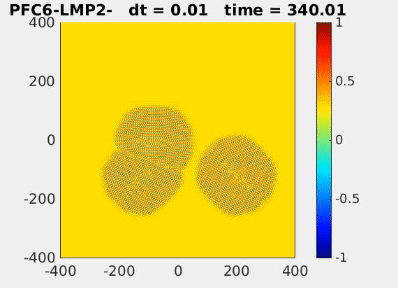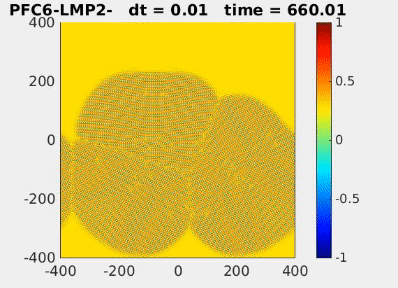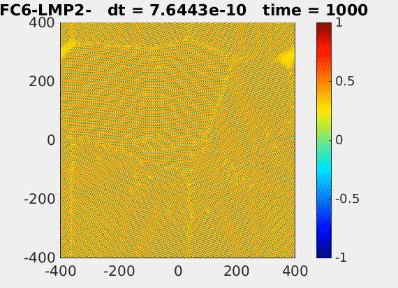 |
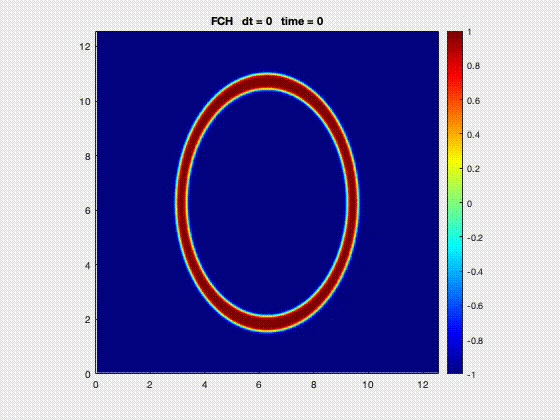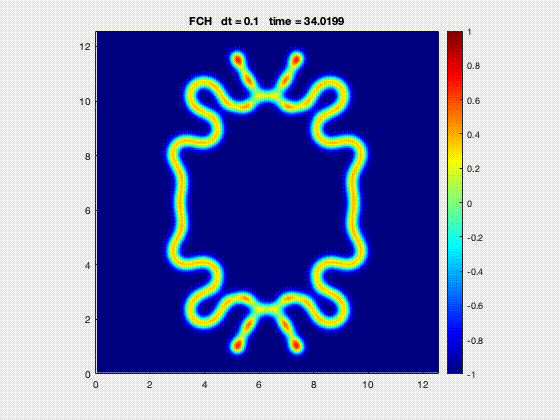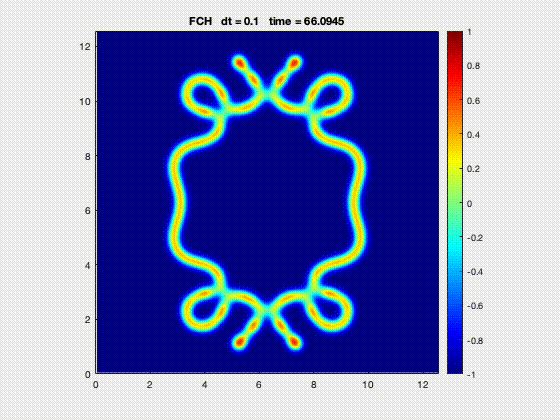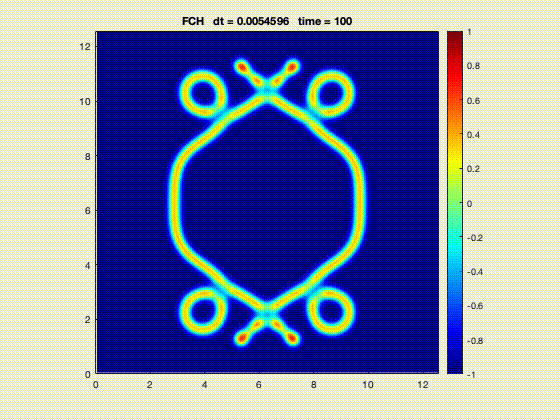
| Evolution of annulus-shaped mixture under Functionalized Cahn-Hilliard model [2] | Crystal formation from grains using the phase field crystal model [2] |
Optimization and its applications to numerical PDEs
[1] Park, J.-H., Salgado, A. J., & Wise, S. M. (2021). Preconditioned accelerated gradient descent methods for locally Lipschitz smooth objectives with applications to the solution of nonlinear PDEs. J. Sci. Comput., 89(1), Paper No. 17, 37. https://doi.org/10.1007/s10915-021-01615-8
Computational study of real world problems
[2] Park, J.-H., Salgado, A. J., & Wise, S. M. (2023). Benchmark computations of the phase field crystal and functionalized Cahn-Hilliard equations via fully implicit, Nesterov accelerated schemes. Communications in Computational Physics, 33(2), 367–398. https://doi.org/10.4208/cicp.OA-2022-0117
[3] (In progress) Park, J.-H., Salgado, A. J., & Wise, S. M. Perturbed preconditioned gradient descent method for Cahn-Hilliard equation with variable mobility.
Theoretical numerical analysis
[4] (in progress) Park, J.-H., Salgado, A. J., & Wise, S. M. Nondegenerate convergence of generic local Lipschitz smooth functionals beyond Sobolev embedding.